|
||||||
 | ||||||
Ｑ17 宇宙船内で円形レールの内側をおもちゃの車が走ると、どうなるだろうか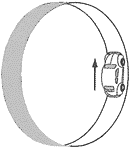？  Ａ17 車の進行方向と反対向きに、レールがまわり出す。車のスピードは次第に落ちていき、車はレールから離れてしまう。 平面上や直線レールの上を、車を走らせようとしてもうまくいかない。車を面に押しつける力がないため、面と車輪との間に摩擦が働かないからだ。 円形レールの内側ならば、はじめに勢いをつければ、遠心力が車をレールに押しつける。すると、固定されていないレールは、車輪とレールの摩擦力の反作用で、車の進行方向と反対向きにまわり出すのだ。 「宇宙船内では、摩擦がなくなる」という人がいるが、これは全くの誤解。それだったら、宇宙飛行士は、物をつかむことができなくなってしまう。 摩擦力は、面と面が押しつけられると発生するもので、地上と変わりない。地上と違うのは、重力が物体を面に押しつけないことだ。 ただし、摩擦力は、運動エネルギーを熱に変えてしまう。そのために、おもちゃの車の運動は、長続きしない。するとやがて、車はレールから離れていってしまう。 Ｑ18 宇宙船内で水滴を自転させると、どうなるだろうか？ Ａ18 不安定になり、やがて２つに分裂することがある。 宇宙船内では、水滴は空中を漂うが、表面張力によって、シャボン玉のように球状にまとまる（図１）。 これを２本の串を使って、重心の位置をそのままにしながら、巻きつけるようにすると、空中で自転させることができる。ところが、この自転運動は、不安定で、長続きしない。わずかな振動が拡大し、変形が始まる（図２）。 自転軸に垂直な方向に広がると、遠心力でさらに引き延ばされる。一方で、球状にまとまろうとする働きもあるから、ヒョウタン状になり、やがて分裂してしまう（図３）。
すべての物質は原子で構成され、その性質は、原子の中心にある「原子核」で決まる。ウランは、自然界で最も大きな原子核をもっている。その中で、「ウラン235」と呼ばれるものは、92個の陽子（正の電気をもっている）と143個の中性子（電気をもたない）で構成されている。これが中性子を１個吸収すると、不安定になって、水滴のように振動を始め、２個の原子核に分裂する。これが、「核分裂」だ。 核分裂の際には、中性子が２～３個放出され、それが他のウラン235の原子核に吸収されると、次々に核分裂が起きる。これが「連鎖反応」だ。原子炉では、連鎖反応が制御されて安定した状態で行われる。 水滴と異なるのは、分裂片が強い放射能をもつことだ。 Ｑ19 宇宙船内で紙飛行機はどう飛ぶのだろうか？ Ａ19 まっすぐに飛ばず、円弧を描いて宙返り飛行をする。 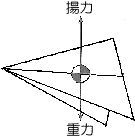 紙飛行機を折るとき、先端の部分を折り重ねるのは、格好良くとがらせるためだけではない。先端部分のおもりの役割のためだ。地上では翼には進行方向に対して垂直に揚力がかかり、重力とのバランスで、姿勢が保たれる。ためしに、紙飛行機の先端部分を折り込むかわりにはさみで切り取ってから、折ってみるとよい。飛ばそうとすると重心のずれに加えて、揚力が過剰となって回転の働きが生じ、上に舞い上がり、すぐに落ちてしまうのだ。翼に生じる揚力は、速度の大きさの２乗に比例する。したがって、重心のバランスがよくとれるように折った紙飛行機でも、速く飛ばしすぎると舞い上がってしまうし、遅いとすぐ落ちてしまう。 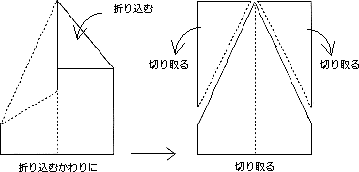 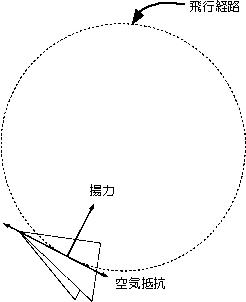 宇宙船内では重力がないから、紙飛行機に働く力は、翼にかかる揚力だけになる。これが円運動するために必要な力（向心力）となり、進む向きから変えられ、宙返り飛行になる。このとき、速度に関係なく、宙返りの円の半径は決まってしまう。向心力は速度の２乗に比例し、半径に反比例する。この場合、翼にかかる揚力が向心力の役割を果たすが、揚力も速度の２乗に比例するので、どんな速度でも一定の半径になるわけだ。 紙飛行機は、一定の半径を保ちながら宙返り飛行をするが、空気抵抗のために次第に遅くなり、やがて宙を漂うだろう。 実際に毛利宇宙飛行士がスペースシャトル「エンデバー号」（STS-47）内で実験した様子をご覧ください。 毛利衛宇宙飛行士の宇宙授業 この実験では、上記の揚力のみによる運動に加え、「重力がないために左右のちょっとしたバランスの違いによってくるくると回ってしまう」効果も確認されました。 他にも、国際宇宙ステーション（ISS）の中で紙飛行機を飛ばしている様子がありますのでご覧ください。 国際宇宙ステーション(ISS)で紙飛行機を飛ばす宇宙飛行士 Ｑ20 国際宇宙ステーションは重さのない宇宙でクレーンを使って組み立てられる。なぜだろうか？ Ａ20 資材の質量が、大きな慣性を持っているため。 ビル建設など、地上の建設現場ではクレーンが活躍する。鉄骨などの骨組みになる資材は重いので、その重力にうち勝って、持ち上げなければならないからだ。 国際宇宙ステーション建設は、巨大な資材を次々に打ち上げ、地球周回軌道上で組み立てる。このとき、クレーンは欠かせない。 ところで、無重力である地球周回軌道で、なぜ、クレーンのような機器が必要になるのだろうか。巨大な資材は、当然、大きな質量を持っている。動かすには、ある程度の加速度を与えなければならないが、質量が大きいということは、それだけ慣性、すなわち「加速されにくさ」が大きいのだ。
だから、巨大な資材を動かすには、大きな力を加える必要がある。小さな力では、とても時間がかかる。また、この理由の方が大切かもしれないが、「加速されにくい」というのは、「止めにくい」ということでもある。組み立ての際に、動き始めた資材同士が衝突して、こわれてしまってはどうしようもない。資材の運動を制御するには、力が必要だ。 宇宙空間では、地上のクレーンのように、フックで引っかけて、ワイヤーでつり下げるわけにはいかない。しっかり資材を固定し、腕も固いものでなければならない。 それと、クレーン本体は、母船に固定されたものでなければならない。さもないと、力を加えても、同時に自分自身も動いてしまうからだ。 Ｑ21 宇宙でアーチェリーをしたい。地上と同じようにできるのだろうか？  Ａ21 無重力の感覚に慣れるまで練習が必要。体も固定しなければならない。 地上で競技をしたとき、重力の影響は避けられない。物体を静かに落下させたとき、ｔ秒後の落下距離は（1/2）gｔ２（g は重力加速度＝9.8m/s２）である。 水平方向に打ち出された矢やボールは重力により、0.1秒後には（1/2）×9.8×（0.1）２ｍ＝4.9cmだけ、鉛直方向に落下しているのだ。１秒後には4.9ｍ、２秒後には19.6ｍになる。 アーチェリーは最大90ｍ離れた的を射る。競技者は、その分を「計算に入れて」やや上向きに打っているはずだ。「計算に入れて」と言ったが、その落下分は経験上、身についているので、意識していないに違いない。無重力では矢は落下せずに、まっすぐ飛んでいくため、慣れるまで練習が必要だろう。 野球のピッチャープレートからホームまで18.44ｍある。横浜ベイスターズの佐々木投手並に150km／ｈの剛速球を投げると、空気抵抗を無視しても、0.44秒はかかる。その間、ボールは95cmも（フォークボールでなくても）落ちるのだ。「浮き上がるような剛速球」というのは、速いために、普通の球よりも軌道が落ちていない、というものの、実際は目の錯覚に過ぎない。それほど、私たちは「慣れ」に支配されているのである。 それと、無重力で大切なのは、体の固定。地上では重力により、地面との摩擦があるが、無重力ではそれがなくなってしまう。「作用反作用の法則」から、矢を打てば、弓から逆向きの力を受けるため、体を固定しないと飛ばされてしまう。宇宙船内では、コンピュータのキーボードをたたくときでさえ、足を固定しないと、反作用で体が動いてしまうので要注意だ。 Ｑ22 宇宙船外で船外活動をする。宇宙船は高速で運動しているのに、宇宙飛行士は取り残されないのだろうか？ Ａ22 宇宙飛行士も等速度で動いているから、大丈夫である。 宇宙船内で宇宙飛行士は、宇宙船と同じ速度をもっている。その速度は「慣性の法則」から、宇宙飛行士が船外に出ても変わらない。正確には、宇宙船とほぼ同じ軌道上を「人間衛星」として地球を周回するわけだ。 その昔、コペルニクスが唱えた地動説を支持したガリレイが、その著書の中で、議論を展開している。天動説の支持者は、落下物体が真下に落ちることを、大地の不動の根拠としている。ところが、等速度で進む船のマストの上から落とした物体は、船が止まっているときと同じように、マストの真下に落ちる。物体は落ちる前から、船と等しい水平速度をもっているからだ。マストの真下に物体が落ちることは、船が止まっている根拠にはならない。 電車に乗っている状態を思い出してみよう。0.5秒でも飛び上がれば、新幹線ならその間に30ｍ近く進むが、ちゃんと飛び上がった床面に着地できる。もっとも、電車が等速度運動しているときに限るが…。 だからといって、命綱なしでよいわけではない。わずかな「ずれ」から、次第に宇宙船から離れて、戻れなくなることはあり得る。命綱は絶対必要だ。 命綱が切れてしまったとき、どうすれば宇宙船に戻ることができるだろう。何でも、持っているものを宇宙船と逆向きに投げればよい。「運動量保存則」から、投げた逆向きの運動量をもつことができるのだ。
Ｑ23 宇宙船内で地上と同じように演奏ができない楽器は、次のうちのどれだろうか？ (1)グランドピアノ (2)トランペット (3)尺八 Ａ23 (1)グランドピアノ。 ピアノは、弦をハンマーでたたいて音を出している。鍵盤をたたくと、その力がハンマーに伝わるが、ハンマーはそのままの勢いで弦をたたき、弦に跳ね返される。跳ね返されたハンマーは、スタンドピアノならバネの力で元にもどるのだが、グランドピアノは重力がないと、何回もハンマーが往復して、続けて弦をたたいてしまう。 参考までに、楽器の音が聞こえるというのは、弦の振動や管内の空気の振動が空気を伝わって耳に伝わるためだ。トランペットなどの管楽器は、管内の空気が振動している。現在、スペースシャトルなどでは、地球上と同じ空気で満たされているから、音の出る条件は全く変わらない。 かつて、地上の空気より酸素の割合を高くしていたこともあるが、そうするとどうなるだろう。地上の空気は酸素が約２割、窒素が約８割だが、酸素の方が窒素よりもわずかに重い。酸素の割合が高いと、管内での空気の振動が伝わる速度が遅くなり、その結果、音程が低くなる。たとえば、空気を100％の酸素に置き換えると、同じ温度で比べれば、管楽器の音程は約半音（ピアノの白鍵と黒鍵の差）だけ低くなる。少し前に流行した、ヘリウムガスを吸って話をすると音声が変わってしまうのも、ヘリウムが空気よりも軽いためなのだ。 ところで、楽器を演奏しても当然ながら空気のない宇宙船外には聞こえない。ＳＦ映画やアニメで宇宙船外での爆発音が聞こえる場面があるが、全くナンセンス。でも音をなくしてしまったら、さぞ退屈な映画になるだろう。
コラム 3 「人工衛星のパラドックス」 地上数百kmの高度の円軌道を描いている人工衛星も、わずかに残る空気抵抗を受けている。ところが、この影響によって、速度は減少するのではなく、逆に増大するのだ。これは「人工衛星のパラドックス」と呼ばれるが、どうしてこのようなことが起きるのだろうか。 実はこれは、「エネルギー保存則」に関係している（Ｑ７参照）。高いところに物体を持ち上げるには、仕事が必要だ。その結果、高いところにある物体は、低いところよりもエネルギーを持っていることになる。これを「位置エネルギー」という。地球から遠く離れると、万有引力はほとんど０（ゼロ）になるから、いくら離れてもそれ以上位置エネルギーは増えず、右ページの図のようになだらかな曲線の変化をする。 人工衛星の質量をｍ、地球の質量をＭ、軌道半径をｒとすると、位置エネルギーＵは、万有引力定数をＧとして、 円軌道では、速度ｖは  で表されるため、運動エネルギーと位置エネルギーの和、すなわち全エネルギーＥは、Ｅ＝（1/2）ｍｖ２ ＋ Ｕ ＝ －ＧＭｍ／２ｒ となり、グラフの太い曲線になる。←→で示した部分が運動エネルギーである。 これで明らかなように、軌道半径ｒが減少すると、全エネルギーＥは減少するが、位置エネルギーＵが２倍減少するため、その差額の運動エネルギーは逆に増加することになる。 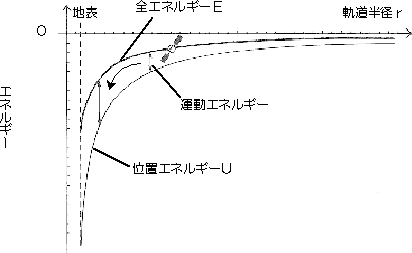 「空気抵抗で速度が増大する」と言っても、エネルギーを失って高度が下がっていくので、少しずつ軌道修正が必要なのだ。そのための燃料がなくなったときが、人工衛星の寿命である。 コラム 4 「無重力」と「無重量」 スペースシャトル内で、浮かんでいる物や宇宙飛行士の姿を映像で見ることは、珍しくなくなった。全く重力がなくなってしまったように見えるが、きちんと理解している人は少ない。「まわりに空気がないから」という誤りに始まって、いちばん多い誤解は、「地球から遠く離れてしまって、地球の支配から逃れている」というものだ。 実は、「Ｑ６」のように、スペースシャトルは、地球に落下しつづけていて、船内は無重力だが、その高度での重力は地上の90％もあるのだ。月までだって、地球の重力は及んでいる。「Ｑ８」でふれたが、スペースシャトルは地球の重力にまかせきった運動なのだ。そこで、「"無重力"というと正しくないから、"無重量"と呼ぼう」という考え方があり、マスコミの一部も"無重量"で統一しているものもある。 ところで、地表で通常、「重力」と呼んでいるものは、測定地点によって異なるものだ。その最大の原因は、緯度による違いで、地球自転の遠心力が、わずかながら異なるためだ。 地球自身が中心に向かって引っ張る力と、遠心力の合力を「重力」として扱うならば、スペースシャトルの内部は「無重力」と表現してもよいわけだ。現実に、アインシュタインの相対性理論においては、実際に働く重力と、加速度運動によって生じる見かけの力は区別できず、同一のものとされる。神経質になるなら、これも「無重力環境下において、物体は無重量に陥る」というべきだ。 「無重力」という表現は、用語としては親しまれているものの、宇宙は薄い大気の抵抗による宇宙船などの減速や、宇宙飛行士が宇宙船内を動くことなどにより「慣性力」が生じ、完全な無重力とはならない。厳密には「微小重力（マイクログラビティ）」と呼ばれている。 コラム 5 「慣性力」と「遠心力」 物体がそのままの状態を続けようとする性質を「慣性」という。力が働いていない物体が、静止ないし等速直線運動をするのが「慣性の法則」だ。 ある観測基準（これを「座標系」と呼ぶ）にとって、「慣性の法則」が成り立っているとき、観測者のいる座標系は「慣性系」と呼ばれる。慣性系においては、物体には力に比例した加速度が生じる。 ところが、慣性系に対して加速度運動する座標系では、「慣性の法則」が成り立たない。 慣性系で静止ないし等速直線運動する物体に対して、加速度運動する観測者が見れば、逆に加速度運動して見える。力が働いていない物体が、加速度運動するのだから、「慣性の法則が成り立っていない」というわけだ。 ところが、同じ観測者が、あくまで慣性の法則が成り立っていると考えたらどうなるだろう。 「加速度が生じているのだから、力が働いている」と考えたとしてもおかしくはない。急ブレーキをかけた電車内で前につんのめるとき、「前に力が働いた」と考えた方が自然なこともある。これが「慣性力」であり、Ｑ８で扱った「見かけの力」の正体だ。 物体の加速度ａが決まれば、運動方程式 ｍａ＝Ｆ より、質量ｍと力Ｆは比例するので、慣性力は必然的に、その物体の質量に比例する。 回転運動の場合は、どうなるのだろうか。 半径ｒの円周上を速度ｖで回転運動する物体は、中心向きに加速度 ｖ２／ｒ の運動をしていることになる。このとき、回転運動する座標系では、見かけの上では中心と反対向きに ｍｖ２／ｒ の慣性力が働くように見える。この回転座標系における慣性力が「遠心力」である。 一般に言われているように、「回転する物体には、遠心力が働く」というのは誤りである。遠心力の原因は、観測者にあるのであって、物体ではない。 コラム 6 「特大プリン」 直径何ｍもあるような特大プリンやゼリーを作ってみたいと思ったことはないだろうか。宇宙ならそれが可能だ。しかし地上ではある程度の大きさになると、自分の重みでつぶれてしまう。 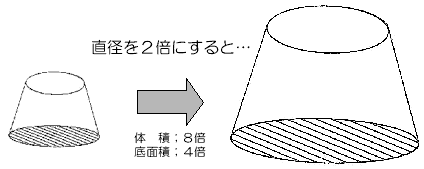 直径２倍のプリンを作るとする。すると底面積は２×２＝４倍に、体積は２×２×２＝８倍になる。密度が変わらなければ、質量は体積に比例するから、底面は４倍の面積で８倍の重みを支えることになり、２倍の圧力がかかる。 直径を10倍にすれば、底面の圧力は10倍になって、柔らかいプリンは、崩れてしまう。 では、天井に届くような、豪華なウェディングケーキはどうなっているのだろうか。 新郎新婦がナイフを入れる部分は本物だが、実は、本体のほとんどは発砲スチロールでできている。スポンジケーキだけでは、重さを支えきれないのだ。 そういう意味では、古代の恐竜やマンモスも、足の負担が大きかっただろう。陸上では背骨をもたない動物で、あまり大きなものが見あたらないのも、うなづける。地球外に生物がいれば、その天体の重力の大きさで、生物の大きさは制約されることが想像できる。 最終更新日：2000年 3月 9日
|
|
