|
||||||
Masayuki Goto1, Kenichi Shida1, Hiroshi Kawamura1 and Shinichi Yoda2
1Science University of Tokyo, 2641 Yamazaki, Noda-shi, Chiba 278-8510, Japan
2National Space Development Agency of Japan, 2-1-1 Sengen, Tsukuba City, 305-8505, Japan
Numerical simulation concerning the thermocapillary convection in a half-zone liquid bridge was conducted. Static and dynamic surface deformations were taken into account in the simulation. The surface deformations are caused by the thermocapillary-driven flow as well as the gravity. In this research, the fundamental equations and the boundary conditions were derived for the concerned configuration with considering the static 2-D and with the dynamic 3-D free-surface displacements. Then, (1) code validation concerning the moderate and the high Prandtl-number fluids and (2) a series of numerical simulation concerning the moderate Prandtl number fluid were conducted.
In the code validation the critical Marangoni number and fundamental frequency of the induced flow in the case of the moderate Prandtl number fluid were compared with the results of the linear stability analysis (LSA). The calculated values were in good agreement with those obtained by LSA. Effect of the dynamic surface deformation upon the critical condition of transition was examined for the moderate Prandtl-number fluid; and its effect has been found rather small. The critical Marangoni number with dynamic surface deformation exhibited slightly higher value than the one obtained by the linear stability analysis. In addition, the calculation of the relative displacement induced by a weak thermocapillary convection of the high Prandtl-number fluid was conducted in order to make a comparison with the experimental results. The numerical results exhibited a quite good agreement. As for the analysis concerning the high Prandtl number fluid, the effects of the numerical mesh size upon the flow field for the various Marangoni- and Prandtl-number fluids were investigated. The special attention was paid upon the velocity and temperature fields at both end corners. As the results, a criterion was obtained for the required mesh size to resolve the large axial velocities and temperature gradients.
In the simulation with the moderate Prandtl number fluid, the critical Marangoni number with and without considering the dynamic surface deformation was obtained. In addition, the phase differences among the surface deformation, the axis- and azimuthal-velocity, and the surface temperature variation were analyzed. It was found that the rotating oscillatory flow retained a lower fundamental frequency than the pulsating one, which was also indicated by the terrestrial experiments.
Fig. 1 indicates the free surface shape without Marangoni convection. The blue line represents the experimental result given by from Nishino. The experimental conditions are: 5cSt of silicone oil as the test fluid, D=5mm, aspect ratio is 0.5, volume ratio is 1.048. The figure shows that the difference between experiment and numerical simulation is enough small and maximum difference is less than 5 %. Especially, the maximum and minimum deflection points agree well each other.
The critical Re number is calculated to investigate the effect of the dynamic free surface deformation for the critical condition. The black line in Fig.2 indicates the absolute azimuthal velocity variation in each Re number without the dynamic free surface deformation under zero gravity. The test fluid is Acetone(Pr=4.4). We calculated in various Re numbers(1000, 1300, 1500, 2000). As for the liquid bridge with dynamic free surface deformation, the azimuthal velocity variation is shown as blue line in Fig.2. The influence of Ca number is one of important parameters for surface deformation. Ca number is defined as the ratio of thermal coefficient of surface tension times delta T divided by surface tension. That is Ca number is 0 in the case of non-deformed liquid bridge. In the case of deformable surface, the increase of delta T results in the increase of both Re and Ca numbers. The relation in the present calculation is Ca = 2.062 x 10-3 and 4.117 x 10-3 at Re = 1000 and 2000, respectively. In the case of the dynamic free surface deformation, the critical Re number is slightly larger than the one with the static free surface. The effect of dynamic free surface deformation can be seen quite small in the present condition.
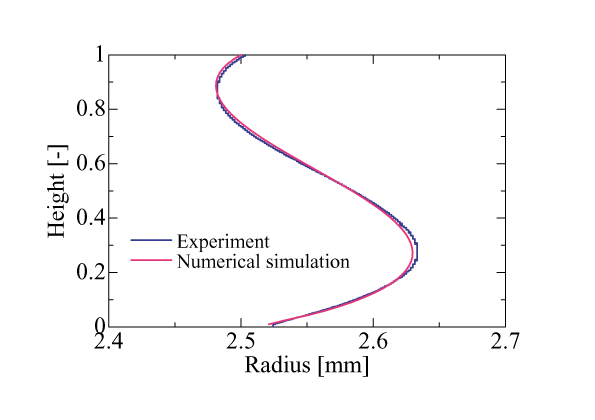
Figure. 1 The shape of liquid bridge for n = 5 cSt, Ar = 0.5, V/V0 = 1.048 and DT = 0 oC
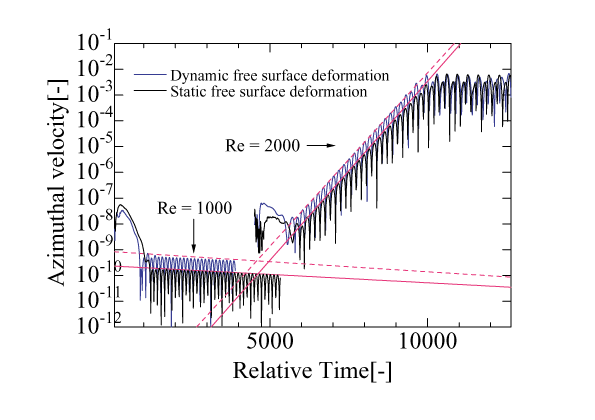
Figure. 2 The azimuthal velocity variation in several Re numbers for Acetone (Pr=4.4), Ar = 0.5, V/V0 = 1.0 and g = 0
Movie File (3.5MB)
 Surface Deformation
Surface Deformation

|